Dans les coulisses de l’ordinateur quantique topologique


Bernard Ourghanlian
CTO et CSO de Microsoft France
Le mois dernier, Microsoft a annoncé un nouveau langage de programmation quantique mais a aussi évoqué de manière un peu plus « grand public » son approche très originale de l’informatique quantique appelée « informatique quantique topologique » permettant de simplifier la résolution de la problématique de la décohérence quantique. Nous allons dans les prochaines lignes tenter de démystifier cette notion d’informatique quantique topologique.
La bataille contre la décohérence quantique
Aujourd’hui, l’état de l’art en matière de calcul quantique se résume – peu ou prou – à quelques mises en œuvre plus ou moins expérimentales de circuits quantiques avec lesquels on peut effectuer quelques opérations élémentaires portant sur un nombre limité de qubits. L’ordinateur quantique envisagé par Google d’ici à la fin de l’année comporterait « seulement » 49 qubits. Certes, un tel ordinateur quantique apporterait « suprématie quantique » mais on reste encore très loin des quelques centaines ou milliers de qubits qui seraient nécessaires pour tenter d’apporter une réponse à quelques-uns des défis les plus importants auxquels fait face notre humanité.
Mais pourquoi les ordinateurs quantiques font-ils face à de telles difficultés pour incorporer davantage de qubits ? Le lecteur intéressé par une présentation générale de ces défis pourra regarder la vidéo de l’un des pères de l’informatique quantique topologique, Michael Freedman. Essayons d’en présenter quelques-unes.
L’idéal serait de pouvoir augmenter le nombre de qubits autant que nécessaire sans pour autant que le temps de cohérence s’en trouve diminué ni que la capacité d’identifier des qubits perde en précision. C’est cette propriété de passage à l’échelle – en anglais scalability – que l’on cherche à atteindre ici. Avant d’exécuter tout calcul, il est nécessaire que le système quantique soit dans un état initial bien défini. Généralement, on cherche à ce que tous les qubits soient dans l’état logique |0>. Cela peut prendre un certain temps lorsqu’il s’agit d’un processus fondé sur le phénomène de relaxation thermique. Mais le plus important, c’est la fidélité avec laquelle l’état initial est préparé dans un état donné.
Tout système quantique interagit avec son environnement et c’est ce qui a pour conséquence de provoquer ce phénomène de décohérence quantique dont nous parlions auparavant et dont la conséquence est la perte d’information sur les phases relatives dans les superpositions d’états. Il importe donc que le déroulement des calculs soit achevé avant que l’information ne soit dégradée. Ceci veut dire que la durée maximale d’un calcul ne peut dépasser un temps T pendant lequel le système demeure cohérent au sens quantique du terme. Or, si l’on désigne par t le temps requis pour l’exécution d’une transformation unitaire élémentaire réalisée par une porte logique agissant sur un qubit, le nombre maximum de telles opérations que l’ordinateur est donné par le rapport n = T/t. Ce rapport dépend de la technologie utilisée pour le mettre en œuvre.
Le tableau ci-dessous donne une idée des performances comparées de différentes approches technologiques pour réaliser un ordinateur quantique :
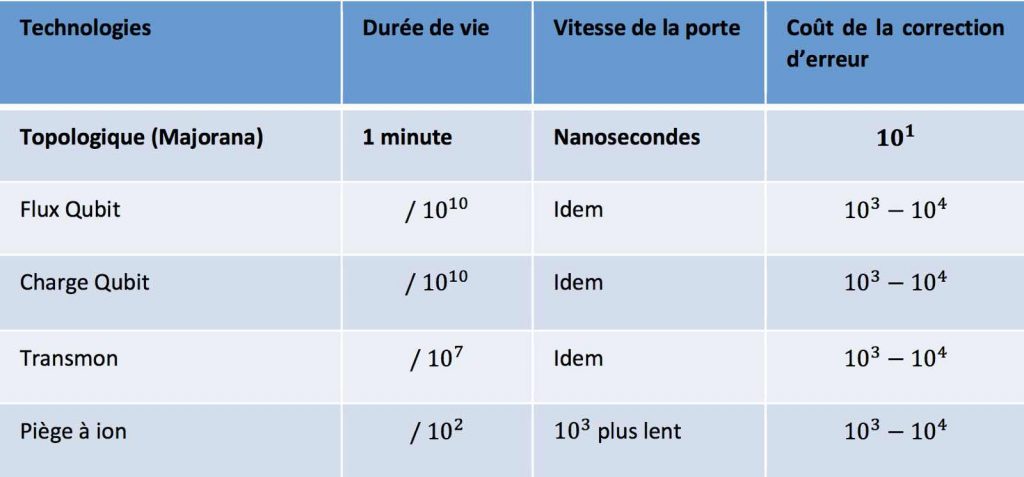
On comprend aisément à la lecture de ce tableau l’avantage que revêt un ordinateur quantique topologique. Essayons maintenant de comprendre de quoi il s’agit.
Aux origines de l’ordinateur quantique topologique
Comme on vient de le voir, toutes les réalisations d’ordinateurs quantiques souffrent d’un mal endémique : leur extrême fragilité qui résulte de la décohérence quantique. Il en résulte des erreurs qui s’introduisent dans les calculs ; d’où le besoin tout à la fois de minimiser les interactions des bits quantiques (les qubits) avec le monde extérieur mais aussi, ainsi qu’évoqué dans le tableau ci-dessus, de mettre en place un mécanisme de correction d’erreur permettant de rectifier le calcul après avoir détecté l’erreur.
Les chercheurs ont prouvé que, si l’on parvenait à diminuer le taux d’erreur à environ une erreur toutes les 10 000 opérations, il serait possible de mettre en œuvre de telles procédures de détection d’erreur pour juguler les effets de la décohérence. C’est dans le droit fil de l’atteinte d’un tel objectif que naquit l’idée de rechercher de l’inspiration dans la topologie, cette branche des mathématiques qui étudie les objets et leurs propriétés lorsque ceux-ci subissent des déformations continues telles la torsion, l’étirement ou la compression.
Voyons un peu sur quoi repose cette idée. En topologie, une boucle fermée et nouée est différente d’une boucle fermée et non nouée car la seule façon de passer de l’une à l’autre nécessite de couper le brin et de recoller ses bouts après avoir défait le nœud.
Dans le calcul quantique topologique, des structures topologiques distinctes correspondent à des états quantiques distincts et l’on cherche – comme avec notre boucle – à tresser des « brins » afin de réaliser le calcul quantique. En fait, ces brins ne sont pas matériels, puisqu’il s’agit des lignes d’univers de certaines particules, c’est‑à-dire de leurs « trajectoires » dans l’espace-temps.
Comme on va le voir dans la suite, pour concevoir un ordinateur quantique topologique, on a recours à des quasi-particules. En physique, les quasi-particules et les excitations collectives (qui sont étroitement apparentées) sont des phénomènes émergents qui se produisent lorsqu’un système microscopiquement compliqué tel qu’un solide se comporte comme s’il contenait différentes particules interagissant faiblement dans l’espace libre. Par exemple, lorsqu’un électron se déplace à travers un semi-conducteur, son mouvement est perturbé de façon complexe par ses interactions avec tous les autres électrons et noyaux ; cependant, il se comporte à peu près comme un électron avec une masse différente (masse effective) voyageant sans perturbation à travers l’espace libre.
Cet « électron » de masse différente est appelé « quasiparticule d’électrons ». Nous n’utilisons pas des particules à proprement parler mais un certain type d’excitations qui surviennent au sein d’un gaz bidimensionnel d’électrons (on reviendra sur ce caractère bidimensionnel qui joue un rôle fondamental dans tout ce qui va suivre). Dans le cas qui nous intéresse, on va utiliser des quasi-particules appelées « anyons » sur lesquelles on va également revenir. Ce qui nous intéresse dans le cas des anyons, c’est qu’elles ont un comportement analogue à celui des particules mais surtout qu’elles ont les propriétés mathématiques requises pour former les structures topologiques dont on a besoin pour réaliser des calculs à savoir des tresses.
Utiliser des anyons pour calculer en faisant… des tresses
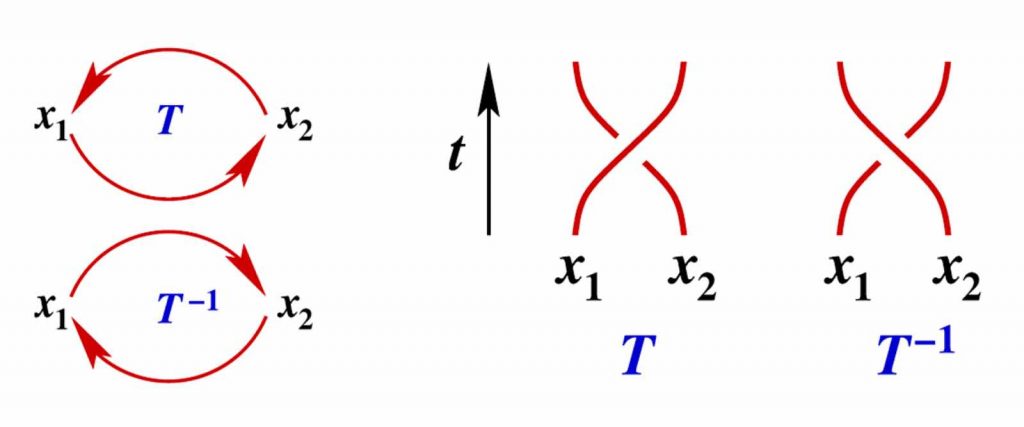
Voyons maintenant comment on peut se servir d’anyons pour faire des calculs. Pour cela, imaginons que l’on crée une paire d’anyons x1 et x2 comme dans le schéma ci-dessous. Dans le cadre de notre ordinateur quantique topologique, chacune de ces paires va jouer le rôle d’un bit quantique. Si l’on fait permuter deux anyons adjacents en les faisant tourner l’un autour de l’autre dans chacun des deux sens possibles T et T-1, cette opération, transcrite en termes de ligne d’univers, produit une tresse élémentaire à deux brins car l’évolution dans le temps de chaque anyon correspond à une ligne d’univers.
On peut procéder de la même façon avec plusieurs paires d’anyons, c’est‑à-dire avec plusieurs bits quantiques.
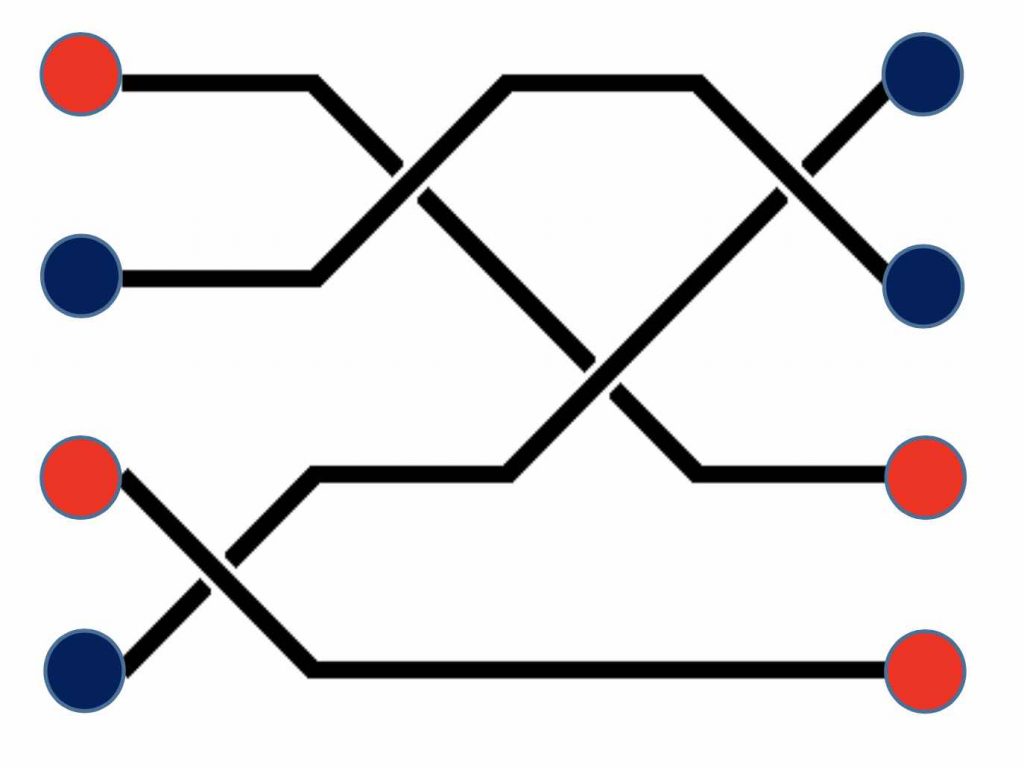
Chaque ligne d’univers d’anyon étant l’équivalent d’un brin, on obtient une tresse particulière qui dépend de la séquence de permutations choisie. L’état final des anyons ainsi obtenu peut être interprété comme le résultat d’un calcul, constitué par le tressage. Voici l’exemple d’une porte quantique de type CNOT :
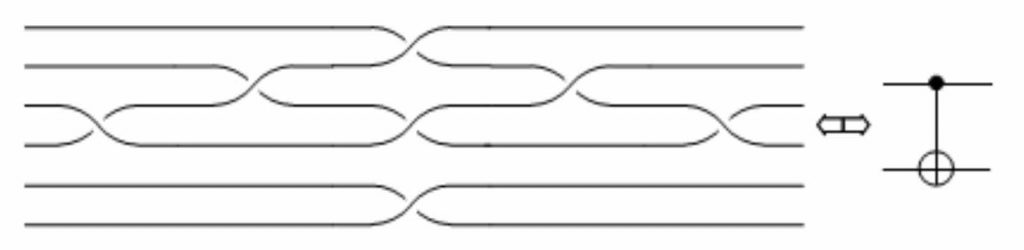
Pour réaliser un calcul quantique, on considère donc que les qubits sont constitués par une colonne de paires d’anyons. Pour effectuer les opérations successives d’un calcul quantique, on échange les positions d’anyons voisins selon une séquence déterminée. Calculer revient donc à tresser des lignes d’univers d’anyons. Les paires d’anyons adjacents résultant du tressage représentent les qubits tels qu’ils ont été transformés par le calcul.
Ici, le résultat ne dépend que de la structure topologique de la tresse (nombre, ordre, nature des permutations) et n’est pas modifié par les petites perturbations dues à l’environnement du système quantique. Un peu comme une corde comportant des nœuds et qui préserverait l’emplacement de ces nœuds malgré la torsion ou l’étirement.
On perçoit ici tout l’intérêt du calcul quantique topologique car la topologie de la tresse, c’est‑à-dire l’agencement des brins les uns par rapport aux autres, n’est pas sensible à des déplacements de brins dus à l’influence du monde extérieur. Un peu comme les quipus mayas qui avaient l’avantage de ne pas avoir à craindre du vent ou de la pluie :
C’est Alexei Kitaev qui travaillait alors au sein de Microsoft Research qui a proposé pour la première fois cette idée de calcul quantique à base d’anyons. C’est ensuite le mathématicien Michael Freedman qui reçut la médaille Fields (l’équivalent du prix Nobel de mathématique) pour son travail sur la conjecture de Poincaré et qui dirige aujourd’hui Microsoft Quantum – Santa Barbara (Station Q), qui fut le premier en 1998 à donner un exposé sur la possibilité d’exploiter des propriétés topologiques pour le calcul. En 1998, il publia ses idées qui s’appuyaient notamment sur la découverte du fait que les « invariants de nœuds » (en particulier le polynôme de Jones) sont liés à la physique quantique d’une surface bidimensionnelle évoluant dans le temps.
En 2004, après une meilleure compréhension du potentiel de l’informatique quantique topologique, Michael Freedman approchait l’un des patrons de Microsoft – en l’occurrence Craig Mundie, l’Executive Vice-président en charge de la stratégie et de la recherche – pour discuter des investissements potentiels de Microsoft en matière d’informatique quantique. Et c’est ainsi que l’aventure de l’informatique quantique topologique démarrait au sein de Microsoft. Juste deux ans après, en 2006, était créé « Station Q » afin de servir de centre de recherche et d’étude de l’informatique quantique topologique piloté par Michael Freedman.
Depuis, de nombreuses étapes vers la mise en œuvre d’un ordinateur quantique topologique ont été franchies avec succès. Dès 1997, Alexei Kitaev commençait à évoquer l’intérêt des anyons et de l’effet Hall fractionnaire pour mettre en œuvre une telle approche. Mais, avant d’aller plus loin, commençons par donner une définition simple d’un anyon.
Les mystérieux anyons
La statistique d’échange en mécanique quantique est un concept ayant des répercussions fondamentales en physique. Dans notre monde à 3 dimensions spatiales, les particules élémentaires peuvent se classer en deux catégories distinctes, appelées bosons et fermions.
Rappelons qu’un système quantique est décrit par ce que l’on appelle une « fonction d’onde » qui est une fonction du temps et de l’espace dont le carré donne la probabilité de présence du système et qui détermine les probabilités d’obtenir un résultat quand on mesure une grandeur de ce système (énergie, position,…). La fonction d’onde qui décrit une paire d’électrons dispose d’une propriété remarquable : en vertu du principe d’exclusion de Pauli, elle change de signe si l’on permute les deux électrons. Ceci a pour conséquence que les bosses de la fonction d’onde seront transformées en creux et réciproquement lors de cette permutation. Bien entendu, ceci reste sans effet sur le carré de la fonction d’onde et donc sur les probabilités de présence de la paire ou les valeurs d’une quelconque quantité mesurable de ce système quantique.
Par contre, le changement de signe de la fonction d’onde a des conséquences sur l’interférence des électrons de la paire avec d’autres électrons. La combinaison de deux ondes est représentée par la somme de leurs amplitudes respectives : le résultat est donc une onde de plus grande amplitude, là où les bosses coïncident et une onde de plus faible amplitude là où les bosses coïncident avec un creux. Ainsi, au fil des opérations quantiques, les amplitudes associées à tel ou tel état peuvent se compenser, un phénomène nommé « interférence destructive », ou au contraire se renforcer : c’est l’ « interférence constructive ».
Or, si l’on multiplie l’une des amplitudes par un facteur ‑1, on transforme les bosses en creux et réciproquement ; d’où la transformation d’une interférence constructive en interférence destructive et réciproquement. En physique quantique, cette même logique s’applique non seulement à toutes les paires d’électrons que l’on échange mais plus généralement à toutes les paires de fermions identiques, c’est‑à-dire de particules qui, tel le proton, le neutron et d’autres, ont un spin demi-entier (pour ce qui concerne les particules de spin entier, que l’on nomme bosons, la fonction d’onde d’un ensemble de bosons identiques ne change pas de signe lorsqu’on permute deux particules). Ainsi, alors que la fonction d’onde est symétrique sous l’échange de deux bosons identiques, elle est antisymétrique dans le cas des fermions.
Cette dernière propriété a de nombreuses conséquences physiques. Par exemple, les phénomènes de condensation de Bose-Einstein, de superfluidité ou encore de supraconductivité découlent directement du fait que les constituants microscopiques de systèmes se comportent comme des bosons. La nature fermionique des électrons est entre autres choses nécessaire à la formation des atomes et des molécules, donne lieu à la structure de bande des semi-conducteurs et est à la base de plusieurs propriétés des matériaux, telle que la déformation due à l’application d’une force.
Les particules sont limitées à être des bosons ou des fermions en 3 dimensions puisqu’effectuer un double échange adiabatique de deux particules est équivalent à encercler l’une avec l’autre. Or, en 3 dimensions, il est toujours possible de transformer continûment une telle trajectoire en un point, ce qui revient à ne faire aucun déplacement. On ne peut donc pas affirmer de façon non ambiguë si une particule en encercle une autre en 3 dimensions spatiales puisque l’enroulement dépend du point de vue de l’observateur. On en conclut qu’après une transformation de ce type, la fonction d’onde ne peut être modifiée que par une phase de ± 1, pour les bosons et les fermions respectivement.
Les anyons sont des types de quasi-particules dont les fonctions d’onde collectives sont multipliées par une phase complexe (un nombre complexe de module 1 mais qui peut être différent de ‑1 ou +1) quand on en échange deux. C’est là l’origine du mot « anyon », formé à partir du mot anglais « any » pour traduire l’idée que toutes les phases complexes sont possibles, et pas seulement les phases particulières +1 ou ‑1. A noter que des anyons d’un type donné sont caractérisés par une même phase.
Les anyons sont donc des quasi-particules dans un espace à 2 dimensions (on parle également d’un espace à 2 + 1 dimensions dans l’espace-temps). Les anyons ne sont donc ni des fermions ni des bosons, mais comme les fermions, ils ne peuvent occuper le même état. Ainsi les lignes d’univers de deux anyons ne peuvent se couper ou fusionner, ce qui permet à leurs chemins de former des tresses stables dans l’espace-temps.
Revenons-en maintenant à l’existence physique des anyons. Pour créer l’univers bidimensionnel des anyons dans notre monde à trois dimensions, il faut créer un espace à deux dimensions et y confiner des particules. Rappelons qu’au départ de cette quête, il fallait trouver des systèmes physiques quantiques doués de degrés de liberté topologiques insensibles aux perturbations locales pour que l’information portée par ces degrés de liberté topologiques soit à l’abri des erreurs dues à la décohérence.
Malheureusement, la plupart des systèmes physiques n’ont pas de degré de liberté topologiques. Cependant, si l’on considère par exemple un système constitué de deux couches de semi-conducteurs à base d’arséniure de gallium avec, en sandwich, une très fine couche d’un matériau contenant des électrons libres mais confinés dans le plan du matériau, il est possible d’entrevoir une solution à ce problème. En effet, si ledit matériau est soumis à un champ magnétique normal à son plan, tandis que les électrons y circulent, alors une tension apparait de part et d’autre de l’interface. C’est l’effet Hall classique.
A très basse température et sous un champ magnétique intense, on observe que la tension de Hall présente des paliers en fonction du champ magnétique : c’est l’effet Hall quantique qui a valu le prix de Nobel de physique à Von Klitzing en 1985. Sous un champ magnétique encore plus intense, des paliers intermédiaires (dits « fractionnaires ») apparaissent. Lorsque ces charges électriques, transportant le courant, sont contraintes à se déplacer dans un plan, par exemple à l’interface entre deux matériaux semi- conducteurs, le rapport entre courant et tension est alors un multiple du quantum de conductance e²/h. Si de surcroît le champ magnétique est intense et la température très basse (quelques dizaines de millikelvin) le rapport entre courant et tension est une fraction rationnelle du quantum de conductance. Les physiciens ont établi que, dans ces conditions d’apparition d’un effet Hall quantique fractionnaire, certaines excitations du gaz d’électrons à l’interface se comportent… comme des particules (des quasi- particules en fait), dotées d’une fraction de la charge électrique de l’électron. D’autres emportent des unités de flux magnétique, comme si chaque unité de flux faisait partie intégrante de la quasi-particule.
C’est en 2005 que Goldman, Camino et Zhou ont annoncé avoir obtenu la preuve expérimentale que les quasi-particules intervenant dans l’effet Hall quantique sont bien des anyons. Comme nous l’avons vu, c’est en permutant des anyons que l’on crée des tresses de lignes d’univers. En physique classique, la permutation de deux électrons conduit à un état final indiscernable de l’état initial puisqu’il est impossible de distinguer un électron de l’autre. Mais, en physique quantique, les choses sont bien différentes. Ainsi, lorsque deux anyons adjacents échangent leurs positions, ils peuvent le faire de telle façon que leurs trajectoires tournent l’une autour de l’autre dans le sens des aiguilles d’une montre ou dans le sens contraire.
Ces deux trajectoires, dites lignes d’univers forment une tresse élémentaire composée de 2 brins telle que dessinée ci-dessous :
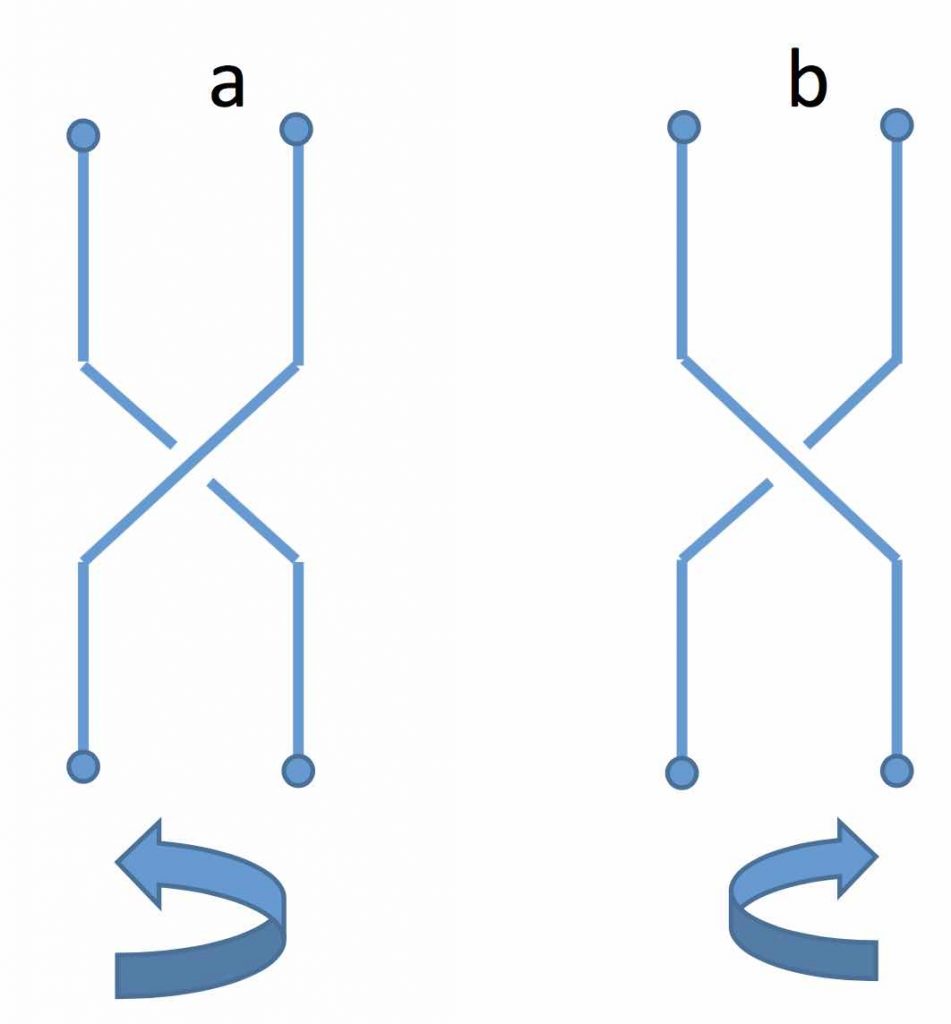
Cette figure représente les lignes d’univers de deux anyons que l’on a permutés en les faisant tourner l’un autour de l’autre en sens inverse du précédent. Notez bien qu’un brin passe au-dessus ou au-dessous de l’autre selon que le sens de permutation direct (a) ou indirect (b), car le facteur de phase en dépend. Les tresses obtenues ainsi sont topologiquement différentes. En effet, le facteur de phase qui vient multiplier la fonction d’onde de la paire d’anyons en dépend.
On peut opérer de la même manière, selon une procédure donnée avec plusieurs paires d’anyons et obtenir une tresse dont la configuration dépend des permutations choisies. Si on associe un qubit à chaque paire d’anyons, l’état des anyons peut s’interpréter comme le résultat d’un calcul effectué par le tressage. La robustesse de ce calcul tient dans le fait que la structure topologique de la tresse constituée par les lignes d’univers du groupe d’anyons est indépendante de la forme de ces lignes et à l’abri des interactions avec l’environnement, car la façon dont la tresse est nouée ne peut changer.
En fait, la construction d’un calculateur quantique topologique nécessite que les anyons disposent d’une propriété supplémentaire : ils doivent être non abéliens, ce qui signifie que l’ordre dans lequel sont effectuées les substitutions a une importance. Autrement dit, si l’on dispose de 3 anyons identiques situés en X, Y, Z et que l’on permute d’abord les anyons X et Y puis ceux situés en Y et Z, le résultat sera représenté par la fonction d’onde du système initial multiplié par un certain facteur de phase. Mais si l’on permute d’abord les anyions placés en Y et Z, puis ceux placés en X et Y, il y aura deux cas possibles : (1) le résultat est représenté par la même fonction d’onde du système initial multipliée par le même facteur que précédemment et les anyons sont dits abéliens, (2) dans le cas contraire, les anyons sont dit non abéliens. Ce caractère non abélien se traduit par le fait que pour de tels anyons, le facteur qui multiplie la fonction d’onde devient une matrice et non plus un nombre complexe de module 124. Or, la multiplication de deux matrices dépend, en général, de l’ordre des facteurs (en général, la multiplication des matrices est en effet non commutative).
A partir du moment où l’on dispose d’anyons non abéliens, il devient possible de décrire une représentation physique du « groupe des tresses », la structure mathématique qui décrit toutes les façons possibles de tresser des brins alignés. N’importe quelle tresse peut être réalisée à partir d’une série d’opérations élémentaires d’inversion des positions de deux brins adjacents, soit dans le sens des aiguilles d’une montre, soit dans le sens opposé. Chaque séquence possible de permutations d’anyons correspond à une tresse et inversement. De cette façon, une matrice de nombres (on parle ici de matrice topologique) est associée à chaque tresse, matrice qui résulte de la multiplication de toutes les matrices individuelles associées aux substitutions successives.
Il nous est maintenant possible de décrire le fonctionnement d’un ordinateur quantique topologique. L’état d’un tel ordinateur est représenté par l’état combiné de tous ses bits quantiques, lesquels sont constitués d’une paire d’anyons. Le passage de l’état initial de tous les bits quantiques à l’état final est décrit par une matrice qui multiplie la fonction d’onde de l’ensemble des bits quantiques, la matrice en question étant associée à la tresse particulière correspondant à la série de substitutions exécutant le calcul.
La question de la détermination des tresses en fonction du calcul à effectuer a été abordé en 2005 par Nicholas Bonesteel de l’Université d’Etat de Floride et ses collègues de Lucent Technologies. Cette équipe a montré comment, en tressant six anyons, il était possible de construire une porte logique « NON contrôlé » ou porte CNOT (de l’anglais Controlled NOT) avec une précision de deux pour mille. Cette porte joue un rôle capital en informatique quantique ; en associant cette porte aux rotations individuelles de qubits et à l’opération de mesure quantique de l’état logique (0 ou 1) d’un qubit, on obtient un jeu de portes universel, suffisant pour réaliser n’importe quel calcul quantique.
Dernier point important à mentionner avant de passer à la question de la fabrication d’un tel ordinateur quantique topologique : comme l’ont prouvé Michael Freedman, Alexei Kitaev, Zenghan Wang et Michael Larsen, il est possible de simuler le fonctionnement d’un calculateur quantique topologique avec une précision arbitraire par un ordinateur quantique conventionnel, ce qui a pour conséquence que tout ce qu’un ordinateur topologique peut calculer peut l’être aussi par un ordinateur quantique conventionnel. De plus, plus le niveau de précision requis est élevé, plus la tresse correspondante comprend de substitutions et donc de croisement de brins. Heureusement, la complexité de la tresse augmente cependant assez lentement pour qu’une bonne précision ne soit pas hors de portée.
Il reste maintenant à évoquer la question capitale de la construction physique d’un tel ordinateur quantique topologique.
A la recherche de Majorana
Dès le début des années 2000, une première piste de mise en œuvre d’anyons au sein d’un ordinateur quantique topologique avait été envisagée autour d’une particule étrange : le fermion de Majorana, nommé ainsi en l’honneur du physicien italien Ettore Majorana qui avait émis l’hypothèse de son existence dès 1937 dans le cadre de la physique des hautes énergies. Un fermion de Majorana est un fermion qui est sa propre antiparticule. Sa charge électrique est nulle, son énergie est nulle, la seule chose qui ne soit pas nulle est sa masse ; c’est pourquoi ce fermion a été si difficile à observer.
En physique de la matière condensée, les fermions de Majorana liés peuvent apparaître comme des excitations de quasi-particules (le mouvement collectif de plusieurs particules individuelles) et elles sont régies par des statistiques non-abéliennes. En 2010, les chercheurs de « Station Q » avaient montré en théorie comment cette quasi-particule insaisissable que l’on nomme le « fermion de Majorana » pouvait être aperçue dans un laboratoire. Mais cette particule demeurait toujours insaisissable.
Une recherche intense pour fournir des preuves expérimentales des états liés de Majorana dans les supraconducteurs a finalement livré des résultats positifs en 2012. Une équipe de l’Institut de Nanoscience Kavli de l’Université de Technologie de Delft aux Pays-Bas pilotée par Leo Kouwenhoven, un partenaire de recherche de Microsoft, a rapporté une expérience impliquant des nanofils d’antimoniure d’indium connectés à un circuit avec un contact d’or sur une extrémité et une couche de supraconducteur sur l’autre. Exposé à un champ magnétique modérément fort, le dispositif expérimental a montré une conductance électrique crête à tension nulle qui correspond à la formation d’une paire de particules de Majorana d’états liés, l’une à chaque extrémité de la région du nanofil en contact avec le supraconducteur. Ce type d’état borné avec une énergie nulle a été rapidement détecté par plusieurs autres groupes dans des dispositifs hybrides similaires.
Depuis cette date historique, de nombreuses autres expériences sont venues conforter l’existence du fameux fermion. Ainsi, en 2014, une équipe de l’université de Princeton a affirmé avoir mesuré à l’aide d’un microscope à effet tunnel à basse température des états liés formant une quasi-particule de Majorana aux bords d’une chaîne d’atomes de fer à la surface d’un cristal de plomb supraconducteur. Les fermions de Majorana peuvent également émerger comme quasiparticules au sein de liquides de spin quantique, et ont été observés par des chercheurs du Oak Ridge National Laboratory, en collaboration avec l’Institut Max Planck et l’Université de Cambridge le 4 avril 2016.
Vers un ordinateur quantique topologique
Si l’on se réfère à la récente conférence Ignite de Microsoft, il semble donc qu’un ordinateur quantique topologique soit désormais en visibilité à travers la mise en œuvre des fameux fermions de Majorana, même s’il reste encore un travail d’ingénierie à accomplir. De manière très simplifiée, un tel ordinateur doit réaliser les tâches ci-dessous :
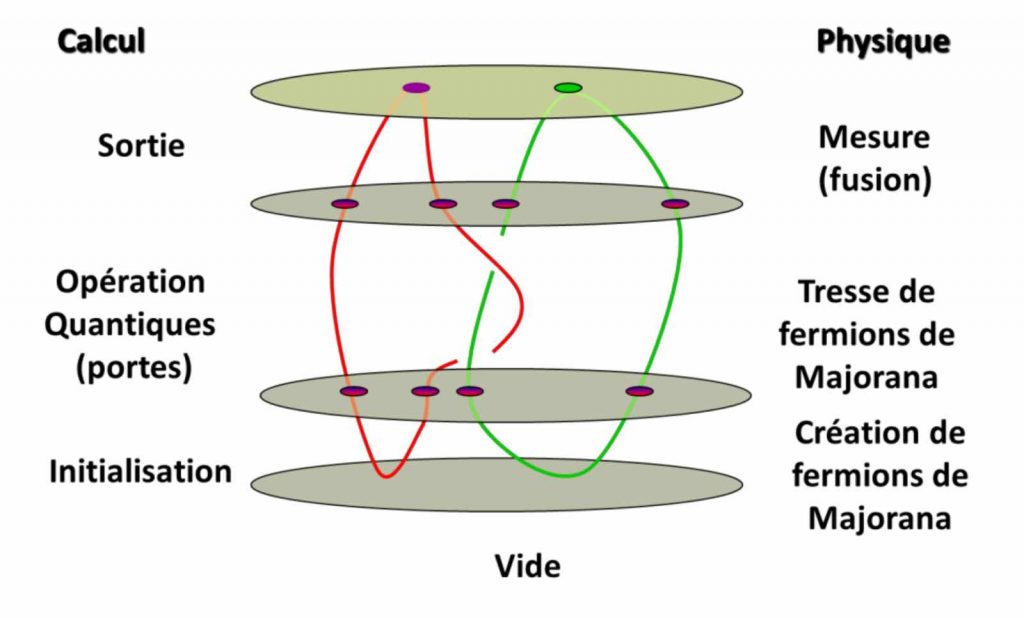
C’est évidemment une illustration extrêmement simpliste du fonctionnement d’un calcul quantique topologique. Lors de l’étape d’initialisation, des fermions de Majorana sont créés à partir du vide ; l’état de qubits est encodé dans l’espace de fusion des paires de fermions de Majorana ; les portes logiques sont par la suite appliquées en tressant les trajectoires dans l’espace-temps des fermions de Majorana ; les fermions de Majorana sont alors fusionnés et les différentes charges topologiques résultantes sont observées.
L’initialisation du calcul quantique peut être effectuée en créant des paires de particules/antiparticules à partir du vide (l’état fondamental du système, caractérisé par l’absence d’excitations). Ceci nous permet de préparer un état connu. Les opérations sont effectuées en tressant les fermions de Majorana, appliquant par le fait même des opérations logiques sur les qubits encodés. La mesure de l’état des qubits encodé dans l’espace de fusion des fermions de Majorana est par la suite obtenue en rapprochant les paires de fermions de Majorana et en mesurant la charge topologique résultante. Le calcul quantique effectué à l’aide de fermions de Majorana (donc d’anyons non abéliens) est naturellement robuste au niveau physique.
Dans ce modèle, l’information n’est pas encodée dans des qubits locaux, mais dans l’espace de fusion d’un ensemble des fermions de Majorana. L’évolution du système obtenu par des opérations de tressage ne dépend pas des détails de la trajectoire dans l’espace-temps des fermions de Majorana, mais seulement de la topologie des tresses ayant eu lieu. L’information encodée étant délocalisée, ceci amène une protection naturelle contre les erreurs causées par l’interaction avec l’environnement, qui ont en général une action locale. Une autre source de robustesse du modèle de calcul quantique topologique provient du fait que les opérations unitaires appliquées sur l’espace de fusion sont discrètes.
En effet, les tresses sont effectuées entièrement ou pas du tout, elles ne peuvent pas être appliquées de manière approximative, étant caractérisées par des propriétés topologiques discrètes des trajectoires. Ceci est en contraste avec les autres systèmes couramment considérés pour servir de qubit. Par exemple, les opérations sur les qubits de spins étant effectuées en appliquant des champs électromagnétiques peuvent comporter une légère imprécision par rapport à l’opération visée, causée notamment par une fluctuation de l’intensité du champ ou de sa durée, et dont les effets s’additionnent avec les applications successives.
Afin de tresser les fermions de Majorana, il est envisagé d’utiliser la même structure de contrôle pour initialiser, tresser et mesurer. La structure de contrôle est de type cryogénique et fonctionne à environ 4°K. Au lieu de déplacer des Majoranas, ils sont couplés et découplés pour les délocaliser et puis les faire apparaitre à l’emplacement souhaité. Tout ceci doit être réalisé de manière adiabatique mais l’avantage d’une telle approche c’est qu’elle peut passer à l’échelle de systèmes bien plus grands.
Lors de la conférence Ignite, Microsoft a également présenté de manière schématique à quoi pouvait ressembler un ordinateur quantique :
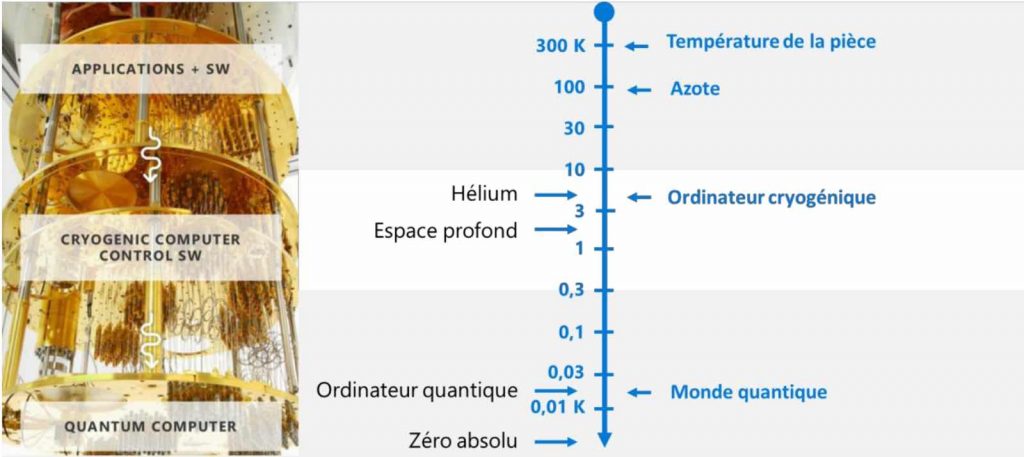
Pour stabiliser l’environnement d’un ordinateur quantique, il faut opérer à très basse température : ‑0,02°K, soit ‑273.13°Celcius. L’ordinateur quantique est contrôlé par un ordinateur cryogénique qui opère dans un contexte de supraconductivité aux alentours de 4°K, soit ‑269,15°C. Le tout est piloté par un ordinateur classique exécutant des algorithmes spécifiques permettant de programmer cet ordinateur pour le moins exotique…
75 ans plus tard
C’est donc sur la base de cet insaisissable fermion dont l’existence n’allait être prouvée physiquement que 75 ans après l’hypothèse de son existence que Microsoft a fondé tous ses espoirs pour créer un ordinateur quantique d’usage général capable, contrairement aux autres technologies disponibles sur le marché, de passer à l’échelle. Un extraordinaire pari fait en se reposant sur les épaules d’un géant, Ettore Majorana.
Pour citer Etienne Klein : « Ettore Majorana m’est « tombé dessus » lorsque je commençais mes études de physique. Ce théoricien fulgurant a surgi dans l’Italie des années vingt, au moment où la physique venait d’accomplir sa révolution quantique et de découvrir l’atome. En 1937, il publia même un article prophétique dans lequel il envisage l’existence de particules d’un genre nouveau, qui pourraient résoudre la grande énigme de la matière noire. Ce jeune homme maigre, aux yeux sombres et incandescents, était considéré comme un génie de la trempe de Galilée. Mais de tels dons ont leur contrepoids : Majorana ne savait pas vivre parmi les hommes, et c’est la pente pessimiste et tourmentée de son âme qui finit par l’emporter. A l’âge de trente et un ans, il décida de disparaître et le fit savoir. Une nuit de mars 1938, il embarqua sur un navire qui effectuait la liaison Naples-Palerme et se volatilisa. »

 Temps de lecture : 20 minutes
Temps de lecture : 20 minutes